Reading: Wooldridge Ch 9
- Theoretical exercise
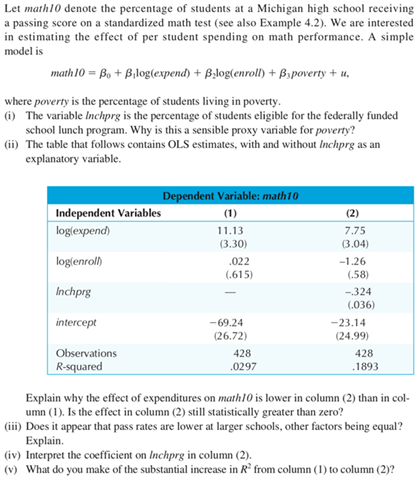
2. Computer exercise.
The dataset JTRAIN contains two datasets, JTRAIN2 and JTRAIN3, which cover the same time period in 1978. JTRAIN2 is the outcome of a job training experiment. The men in this dataset were low earners targeted to receive training in a special job training experiment. JTRAIN3 is observational data on individuals who themselves determine whether they participate in job training. This sample is a random sample from the population of working men.
(i) In each data set, what fraction of the men received job training? Why do you think there is such a big difference?
(ii) Using JTRAIN2, run a simple regression of re78 on train. What is the estimated effect of participating in job training on real earnings?
(iii) Now add as controls to the regression in part (ii) the variables re74, re75, educ, age, black, and hisp. Does the estimated effect of job training on re78 change much? How would you explain it?
(iv) Do the regressions in parts (ii) and (iii) using the data in JTRAIN3, reporting only the estimated coefficients on train, along with their t statistics. What is the effect now of controlling for the extra factors, and why?
(v) Define avgre = (re74 + re75)/2. Find the sample averages, standard deviations, and minimum and maximum values in the two data sets. Are these data sets representative of the same populations in 1978?
(vi) Almost 96% of men in the data set JTRAIN2 have avgre less than $10,000. Using only these men, run the regression
re78 on train,re74,re75,educ,age,black,hisp
and report the training estimate and its t statistic. Run the same regression for JTRAIN3, using only men with avgre <=10. For the subsample of low-income men, how do the estimated training effects compare across the experimental and nonexperimental data sets?
(vii) Now use each data set to run the simple regression re78 on train, but only for men who were unemployed in 1974 and 1975. How do the training estimates compare now?
(viii) Using your findings from the previous regressions, discuss the potential importance of having comparable populations underlying comparisons of experimental and nonexperimental estima


